| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 파이썬
- 프로그래머스
- MySQL
- 코테
- 쿼리테스트
- 데이터분석가
- SQL
- 취업부트캠프
- 실습
- Python
- 회고록
- 유데미
- 자격증준비
- 태블로
- 부트캠프후기
- trouble shooting
- 2024년
- tableau
- 자격증
- 스타터스부트캠프
- Tableau Desktop Specialist
- 데이터시각화
- 러닝스푼즈
- 데이터분석
- AICE
- 유데미코리아
- 유데미부트캠프
- 프로젝트
- 코딩테스트
- 프리온보딩
- Today
- Total
신이 되고 싶은 갓지이
2. Python 머신러닝 - Clustering을 실습을 통해 알아보기(Boston Data), 인코딩 본문
Clustering (군집화)
: 거리별로 데이터를 묶는 작업
1) K-means
- 주어진 값들 사이의 거리 혹은 유사성을 이용하여 분류
- 전체 데이터를 K개의 집단으로 그룹화
- 데이터를 기준점 중심으로 Euclidean 거리가 최소가 되도록 K개의 그룹으로 군집 (맨해튼 등 다른 거리법도 존재)
- 군집 별 중심 값에서 중심과의 거리를 기반으로 데이터를 분류하는 군집기법
- 거리를 이용한 분류로, 범주형 변수를 다루기 좋은 방법은 아님
- 짧은 계산 시가능로 반복된 작업 수행
- 주어진 자료에 대한 사전정보 없이 의미 있는 자료구조 찾기 가능
- 알고리즘 작동 방법
- 초기 K개의 랜덤한 군집 중심 선택
- 값들의 거리를 비교하고 가까운 군집에 할당
- 새로운 군집의 중심 계산
- 재정의 된 중심값 기준으로 다시 거리기반의 군집 재분류, 경계가 변경되지 않으면 종료
- K설정법
- Elbow Point 찾기
- K-means는 오브젝트와의 거리의 제곱합이 비용함수 → 응집도가 줄어든다
- K의 개수는 증가하지만 비용함수의 차이가 나지 않는 부분이 Elbow Point
* 비지도 학습의 특징인 해석하기에 따라 결과값이 매우 다르다. 왜냐하면 Elbow Point가 사람마다 다를 수 있기 때문
2) 실습
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
data = pd.read_csv('./data/boston.csv')
1단계 PCA
군집화를 진행하기에 앞서 수월한 시각화 및 설명력을 첨부하기 위하여 PCA를 통해 변수를 2개로 압축
# 범주형 데이터 제거
del data['chas']
# 나중에 비교를 위한 medv 컬럼도 복사 후 제거
medv = data['medv']
del data['medv']
# PCA
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
scaler = StandardScaler()
scaler.fit(data)
scaler_data = scaler.transform(data)
pca = PCA(n_components = 2)
pca.fit(scaler_data)
pca.transform(scaler_data)
# 데이터프레임 형태로 형태변환
data2 = pd.DataFrame(data = pca.transform(scaler_data), columns = ['pc1', 'pc2'])
2단계 Elbow Point 찾기
몇 개의 군집화로 나누는것이 가장 올바른 군집화인지 살펴보기 위해 Elbow Point를 찾는다.
- KMeans(n_cluster = k)
- k개의 군집화를 하겠다는 객체 생성
- Kmeans.fit(df)
- 학습시키기
- KMeans.inertia_
- 학습된 KMeans의 응집도를 확인
- 응집도란 각 데이터로부터 자신이 속한 군집의 중심까지의 거리를 의미
- 즉, 낮을수록 군집화가 더 잘되어있음.
- KMeans.predict(data)
- 학습된 데이터를 바탕으로 데이터를 변환시켜줌
from sklearn.cluster import KMeans
# Elbow Point를 찾기 위한 for문
x = [] # k가 몇개인지
y = [] # 응집도가 몇인지
for k in range(1,30) :
kmeans = KMeans(n_clusters = k, n_init="auto")
kmeans.fit(data2)
x.append(k)
y.append(kmeans.inertia_)
# 그래프 그리기
plt.plot(x, y)
→ 확인 결과 Elbow Point는 4로 확인된다.
3단계 Clustering
# 객체 생성
kmeans = KMeans(n_clusters = 4)
kmeans.fit(data2)
data2['labels'] = kmeans.predict(data2)
# clustering 결과 시각화
sns.scatterplot(x = 'pc1', y = 'pc2', hue = 'labels', data = data2)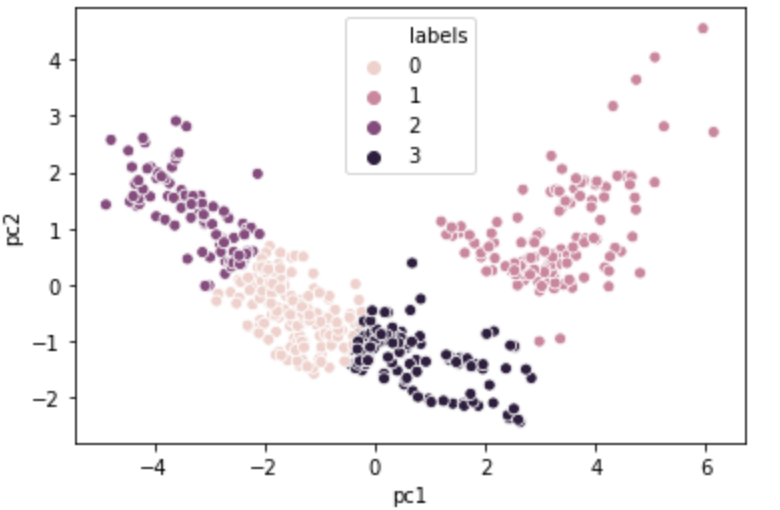
→ K-means는 최초의 기준점을 random하게 찍기 때문에 조금은 다른 결과가 나올 수 있지만 그룹은 비슷하게 나뉠 것이다.
4단계 결과 해석
# 맨 처음 떼어 두었던 medv 컬럼(결과값)을 추가
data2['medv'] = medv
# 시각화를 위해 각 그룹별 medv값을 label별로 변수로 생성
mdedv_0 = data2[data2['labels']==0]['medv'].mean()
mdedv_1 = data2[data2['labels']==1]['medv'].mean()
mdedv_2 = data2[data2['labels']==2]['medv'].mean()
mdedv_3 = data2[data2['labels']==3]['medv'].mean()
# 주의) 모든 과정을 똑같이 하였어도 kmeans의 기본 중심값 설정은 '랜덤'임을 잊지 말 것
sns.barplot(x = ['group_0','group_1','group_2','group_3'],
y = [mdedv_0, mdedv_1, mdedv_2, mdedv_3])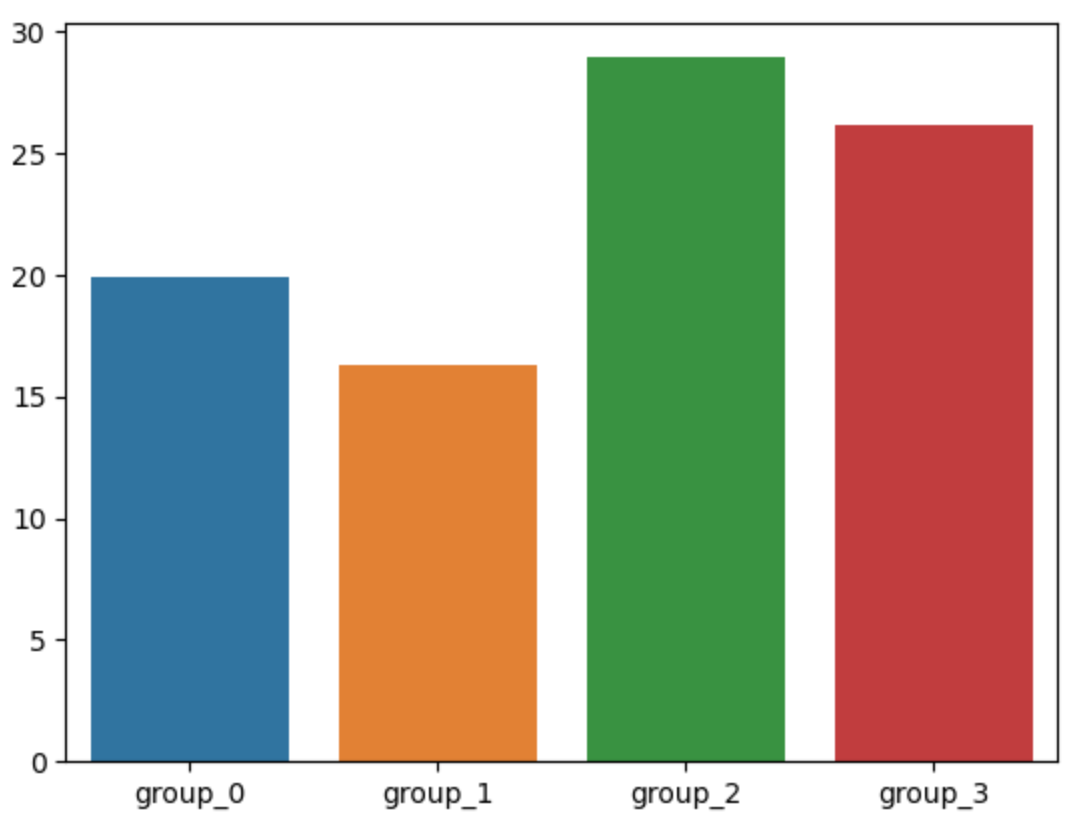
→ group1의 평균값이 가장 낮고, gorup2의 평균값이 가장 높은 것을 볼 수 있다.
5단계 최상위, 최하위 그룹의 특징 확인
# 원본 데이터에 라벨을 복제
data['labels'] = data2['labels']
# 각 그룹의 데이터를 나누어서 변수에 담기
group = data[(data['labels']==1) | (data['labels']==2)]
# pivot 하기
group = group.groupby('labels').mean().reset_index()
# 두 lablel의 변수별 평균값을 그래프로 확인
column = group.columns
# 반복문을 이용
f, ax = plt.subplots(2, 6, figsize=(20, 13))
for i in range(1, 12) :
sns.barplot(x = 'labels', y = column[i], data = group, ax = ax[i//6, i%6])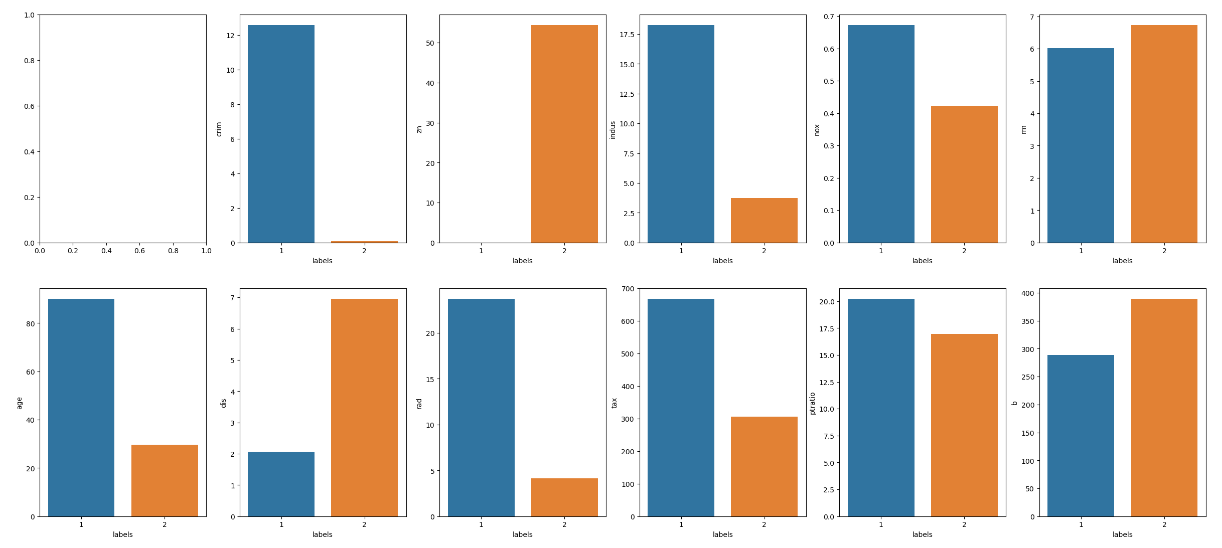
결론
그래프에서 확인 할수 있는 것 처럼 범죄율이 낮을 수록, 25,000 평방피트를 초과 거주지역 비율이 높을수록 좋은 가격을 나타내는 지역임을 알 수 있다. 또한, 두가지 뿐 아니라 여러가지의 그래프를 보고도 집 값이 높은 지역의 특징들을 살펴볼 수 있다.
인코딩
: 머신러닝을 학습시키기 위해서 숫자가 아닌 단어 혹은 문자열을 숫자로 변경해야만 학습이 가능
1. 라벨 인코딩
: 문자열을 카테고리별로 적용시키는 인코딩 방식
ex) 최상위=4, 상위=3, 중간=2, 하위=1
2. 원 핫 인코딩
: 문자열을 숫자로 변경하는 점은 라벨 인코딩과 동일하지만 원 핫 인코딩은 카테고리별로 변경하는 것이 아닌 0과 1만을 소유하는 테이블을 생성해 해당되는 데이터만 1 표시, 해당하지 않는 데이터는 0으로 채우는 인코딩 방식
ex) 최상위 상위 중간 하위
0 0 0 0 1
1 0 0 1 0
2 0 1 0 0
3 1 0 0 0
'Python' 카테고리의 다른 글
| 4. Python 머신러닝 - 지도학습2(의사결정나무)와 실습 (3) | 2024.01.30 |
|---|---|
| 3. Python 머신러닝 - 지도학습1(KNN, 의사결정나무)의 실습 후 모델 성능 측정하기 (2) | 2024.01.25 |
| 1. Python 머신러닝 - 공분산과 상관계수, 차원축소를 실습을 통해 알아보기(Boston Data) (4) | 2024.01.22 |
| 7. Python 기초 - API 활용하여 데이터 수집하기 (6) | 2024.01.19 |
| 6. Python 기초 - 일시를 관리하는 datetime 라이브러리 (2) | 2024.01.15 |



