| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 자격증
- 자격증준비
- 유데미
- 쿼리테스트
- tableau
- 회고록
- Python
- 데이터시각화
- 프로젝트
- 프로그래머스
- 코테
- 러닝스푼즈
- 태블로
- trouble shooting
- SQL
- 유데미부트캠프
- 데이터분석가
- 프리온보딩
- 파이썬
- Tableau Desktop Specialist
- MySQL
- 취업부트캠프
- AICE
- 2024년
- 유데미코리아
- 부트캠프후기
- 데이터분석
- 코딩테스트
- 실습
- 스타터스부트캠프
- Today
- Total
신이 되고 싶은 갓지이
1. Python 머신러닝 - 공분산과 상관계수, 차원축소를 실습을 통해 알아보기(Boston Data) 본문
1. 공분산과 상관계수
1) 특징
- 먄약 x,y가 독립이면 공분산은 0
- 단, 공분산은 x와 y의 크기에 영향을 받기 때문에 상관성은 낮지만 절대적 점수가 높은 공분산이 반대의 경우보다 높게 나올 수 있음
- 상관계수는 공분산의 단점을 보완하여 -1에서 1까지의 범위로 정규화
2) 상관관계와 인과관계
- 상관관계는 두 변수 사이에서 보여지는 상관성만 나타낸것
- 인과관계는 x떄문에 y가 발생
- 회귀분석을 통해 인과관계의 방향, 정도와 수학적 모델을 확인 가능
2. 차원축소
1) 차원축소
: 3차원에서 2차원으로 차원을 줄이는 작업
✔️ 차원축소를 하는 이유
- 시각적 용이함
- 변수의 조합을 통해 새로운 변수 발견
- 단, 데이터 특징이 많아지면 이를 채우기 위핸 데이터 수도 많아야함(오버피팅 문제)
✔️ 차원 축소 방법
1. Feature Selection (변수 선택)
- 갖고 있는 변수중 의미 있는 변수만 선택
- 주로 상관분석을 통해 변수를 선택
2. Feature Extraction (변수 추출)
- 1,2,3번 변수를 조합해서 A,B라는 변수 생성
- 주로 사용되는 방법은 주성분분석(PCA)
- PCA 실행 결과 나온 변수를 그래프로 그린 뒤 급격하게 떨어지는 지점에서 PC 개수 선택
2) PCA (주성분분석)
: 많이 사용되는 변수 추출 방법
- 분산이 최대인 축 찾기 → 데이터 유실을 최대한 일으키지 않는 선(pc1) 찾기
- 찾은 축과 직교하면서 분산이 최대인 두번째 축 찾기 → pc2
- 첫번째 축과 두번째 축에 직교하고 분산을 보존하는 세번째 축 찾기
3) 정규화
- PCA를 위해서는 반드시 정규화가 필요
- 스케일이 다르면 분산이 다름
4) 실습
: boston.csv(보스턴의 집값 데이터)를 통해 실습을 진행한다. 칼럼을 다음과 같고 분석 목표는 공분산과 상관관계를 통해 보스턴의 집값에 영향을 주는 변수를 확인 하는 것이다.

1단계 - Feature Selection1
: 가설을 세워 상관관계 확인
가설1. 범죄율이 높은 곳의 집 값은 낮을까?
* 우선 상관계수와 공분산은 연속형자료를 분석하기 때문에 범주형변수를 제거한 후 진행한다. 단, 데이터 제거는 신중히 확인 한 후 진행해야한다. 보통은 원본에서의 제거가 아닌 사본에서의 제거를 추천한다.
1. 실제 데이터로 그래프 그려보기
* 데이터를 살펴보았을 때 일반적인 상식과 다른 경우가 나오는 데이터가 있을 수 있으므로 실제 데이터로 그래프를 그려본 뒤 가설을 확인해보는것이 중요
# 상관계수와 공분산은 연속형자료를 분석하기 때문에 범주형변수를 제거
del data['rad']
del data['chas']
sns.jointplot(data = data, x = 'crim', y = 'medv', kind = 'reg')- 산점도와 추세선을 함께 볼수 있는 regplot을 통해 가설이 맞는지 확인
→ 결과적으로 가설에 맞게 우하향 하는 것을 확인 해 볼 수 있다.
2. 상관계수와 공분산 확인
- x.cov(y)
- 공분산을 확인하기 위한 함수
- x와 y에 같은 시리즈형의 데이터를 대입
- df.cov()처럼 데이터프레임을 x에 넣고 y자리에 아무것도 적지 않으면 각 변수별로 공분산을 계산
- x.corr(y)
- 상관계수를 확인하기 위한 함수
- x와 y에 같은 시리즈형의 데이터를 대입
- df.corr()처럼 데이터프레임을 x에 넣고 y자리에 아무것도 적지 않으면 각 변수별로 공분산을 계산
# 실제 범죄율과 집 값의 공분산을 확인
data['crim'].cov(data['medv'])
# 실제 상관계수 확인
data['crim'].corr(data['medv'])
→ 공분산은 -30.718507964458173, 상관계수는 -0.38830460858681143로 강한 음의 상관관계를 나타낸다. 따라서 가설이 옳음을 확인 할 수 있다.
1단계 - Feature Selection2
: heatmap을 통해 변수 사이의 상관관계를 확인
- sns.heatmap(df, cmap='YlGnBu', annot=False, fmt="0.1f")
- cmap - 전체적인 색을 지정 (summer / YlGnBu / RdYlGn_r 등)
- annot - True / False 로써 숫자를 표현해줄 것인지 기입
- fmt - 숫자의 소숫점 자리수 설정
plt.figure(figsize=(16,9))
sns.heatmap(data.corr(),cmap='YlGnBu',annot=True,fmt="0.1f")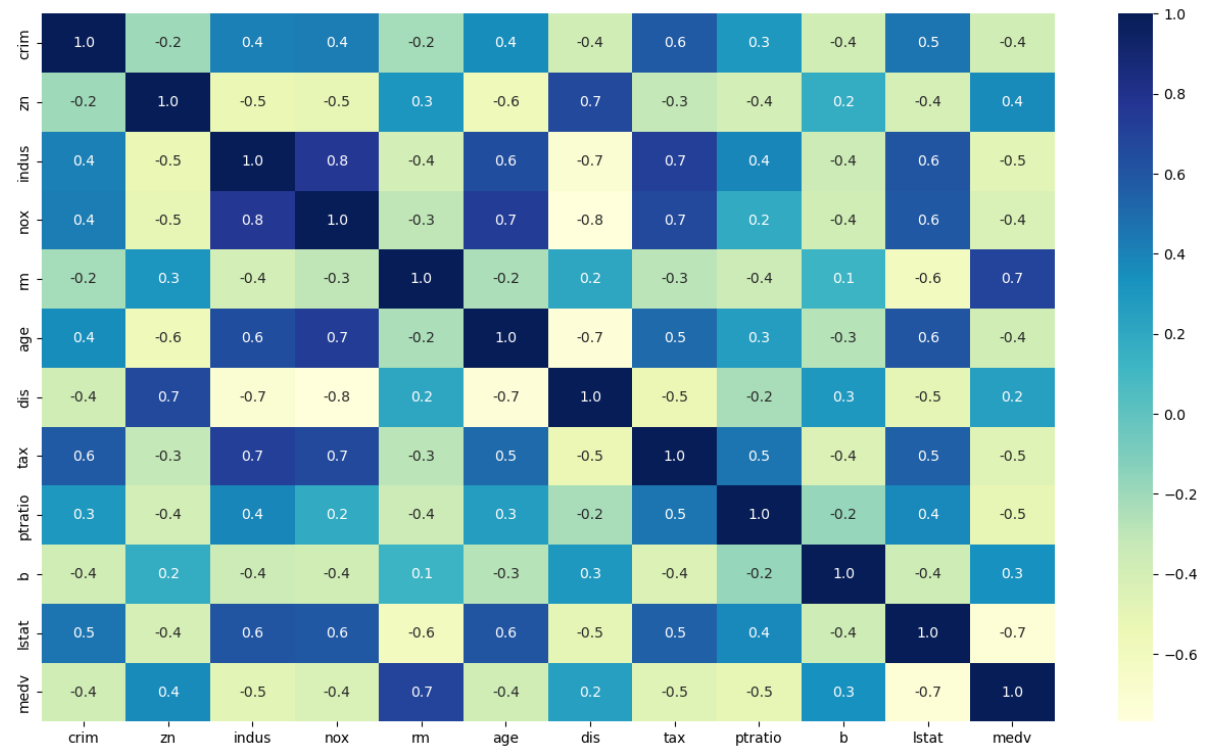
2단계 - Feature Extraction
: PCA를 통해 새로운 변수 생성
변수들의 상관계수를 확인하고 낮은 두 변수는 하나의 변수로 생성하여 상관계수가 높은 새로운 새로운 변수를 생성한다.
1. 변수들의 상관계수 모두 확인
# 변수들의 상관계수를 전부 확인하고 몇개의 변수를 몇개로 줄일 것 인지 확인
corr_bar = []
for column in data.columns :
print(f'{column}과 medv의 상관관계 : {data["medv"].corr(data[column])}')
corr_bar.append(abs(data["medv"].corr(data[column]))) # 절대값을 통해 손쉬운 비교
2. 확인한 상관계수 값을 비교
# barplot을 통하여 그래프를 그려보기
sns.barplot(data.columns, corr_bar)
→ 확인 결과 'dis'와 'b'가 가장 낮은 상관관계를 갖는 것을 확인 할 수 있다.
3. PCA를 통해 2개의 변수를 조합하여 1개의 변수를 만들기
- PCA(n_components = 변수갯수)
- n_components : 몇가지의 변수를 만들지 개수를 정함
- 객체를 생성하는 개념(붕어빵 틀 만들기)
- 아래 4개의 함수를 사용할 수 있는 권한 받는 단계
- PCA.fit(x)
- x의 데이터를 학습시킴으로써 앞에서 생성한 객체가 데이터를 공부하는 개념
- PCA.components_
- 앞서 학습한 내용을 바탕으로 만들어진 변수속에 담긴 이 전 변수의 분산이 담김 정도
- PCA.explained_variance_ratio_
- 새로운 변수가 설명하는 분산의 비율
- PCA.fit_transform
- 학습한 내용을 바탕으로 만들어진 학습기로 x의 데이터를 변환
# PCA를 위한 라이브러리를 불러오기
from sklearn.decomposition import PCA
# 수치형데이터 중에 비교적 상관계수가 낮은 두개의 변수를 선택
x = data[['dis', 'b']]
# 2개의 변수를 조합하여 1개의 변수를 만들기
pca = PCA(n_components=1)
# 데이터를 학습
pca.fit(x)
# 새로운 변수에 담긴 각 변수의 분산을 확인
pca.components_ # array([[-0.00672682, -0.99997737]]) -> dis보다 b가 더 많은 설명력을 갖고있다는 의미
# 새로운 변수 PC1이 설명하는 분산의 비율
pca.explained_variance_ratio_ # array([0.9995135]) -> b가 많이 차지하고 있기에 나온 결과
# 새로운 변수를 pc1이라는 컬럼에 추가
data['pc1'] = pca.fit_transform(x)
# 상관계수도 확인
data['pc1'].corr(data['medv']) # -0.3334845106741898 -> 통합 전 두 변수와 거의 비슷하기에 큰 의미가 없음
3단계 - 정규화
앞서 두 변수를 하나의 변수로 생성하는 과정에서 두 변수의 비율이 상당히 큰 차이를 두고 있다는것을 확인 할 수 있었으며 이에 따라 생성된 새로운 변수의 상관계수가 유의미한 결과값을 내지 못 했다. 이를 해결하기 위해 두 변수의 정규화를 진행한다.
- StandardScaler()
- 정규화 객체 생성
- scaler.fit(x)
- 정규화 객체로 학습
- scaler.transform(x)
- 학습된 학습기로 변수 x의 데이터를 변환
# 정규화에 필요한 라이브러리
from sklearn.preprocessing import StandardScaler
# 정규화 객체를 만들기
scaler = StandardScaler()
# x를 학습시킨 후 변형하여 정규환된 x로 만들기
scaler.fit(x)
scaler_x = scaler.transform(x)
# 앞서 진행한 PCA 반복
pca = PCA(n_components=1)
pca.fit(scaler_x)
pca.components_ # array([[-0.70710678, -0.70710678]]) -> 달라진 분산의 정도를 확인할 수 있음
pca.explained_variance_ratio_ # array([0.64575584])
data['pc1'].corr(data['medv']) # -0.36298985100090175 -> 두 변수보다 상관계수가 유의미하게 변함'Python' 카테고리의 다른 글
| 3. Python 머신러닝 - 지도학습1(KNN, 의사결정나무)의 실습 후 모델 성능 측정하기 (2) | 2024.01.25 |
|---|---|
| 2. Python 머신러닝 - Clustering을 실습을 통해 알아보기(Boston Data), 인코딩 (5) | 2024.01.23 |
| 7. Python 기초 - API 활용하여 데이터 수집하기 (6) | 2024.01.19 |
| 6. Python 기초 - 일시를 관리하는 datetime 라이브러리 (2) | 2024.01.15 |
| 5. Python 기초 - 엑셀 파일 통합 정리 (3) | 2024.01.15 |


